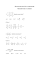projenin adı napoleon teoreminin dikdörtgene uygulanması projeyi

PROJENİN ADI
NAPOLEON TEOREMİNİN DİKDÖRTGENE UYGULANMASI
PROJEYİ HAZIRLAYANLAR
ECEM OBUROĞLU, PELİN ÖZKAN
OKUL ADI VE ADRESİ
ÖZEL KÜLTÜR LİSESİ
Ataköy 9.-10. Kısım,34156 Bakırköy-İstanbul
DANIŞMAN ÖĞRETMEN
SEÇİL SEVİNÇ
PROJENİN ADI: NAPOLEON TEOREMİNİN DİKDÖRTGENE UYGULANMASI
PROJEYİ HAZIRLAYANLAR: ECEM OBUROĞLU,
PELİN ÖZKAN
PROJE DALI:
MATEMATİK
PROJE ÖĞRETMENİ:
SEÇİL SEVİNÇ
PROJE AMACI: Üçgenlerde ispatlanan Napoleon Teoremini kullanarak bu özelliğin dikdörtgende
uygulanabilirliğinin araştırılması.
GİRİŞ: Üçgenlerde sağlanan Napoleon Teoreminin ispatı verilir.
NAPOLEON TEOREMİ
Herhangi bir üçgenin üç kenarının üzerine ister içine,isterse dışına doğru eşkenar üçgenler
çizildiğinde,bu üçgenlerin ağırlık merkezleri birleştirilirse yine bir eşkenar üçgen oluşur.
İspat:
ABC üçgeninin üç kenarının üzerine üçgenin içine/dışına doğru şekildeki gibi BAC,CBA ve
ACB eşkenar üçgenleri yerleştirilirse ve bu üçgenlerin ağırlık merkezleri sırasıyla D,E ve F ise DEF
üçgeni de eşkenardır.
ABC üçgeninde
=a,
=b,
=c ,
=n ,
=m ve
=x ve ABC üçgeninin alanı 
olsun.
AF ve AE içinde bulundukları üçgenlerin
içaçıortay
doğruları
olduklarından
m(
=
dir.Bundan dolayı m(
) = A +
dır.FAE üçgeninde kosinüs
teoreminden,
= +
– 2.m.n. cos(A+
)
(1)
bulunur. m ve n uzunlukları,içinde bulundukları eşkenar üçgenlerin yüksekliklerinin 2/3’ü
olduğundan
m=
ve
n=
tür. Bu değerler (1) eşitliğinde yerine yazılırsa;
=
+
) ‘den
.cos(A+
3
=
+ -2.b.c. cos(A+
)
(2)
elde edilir.
cos(A+
) = cosA.cos
- sinA.sin
değeri (2) de yerine yazılırsa;
3
=
+ -2.b.c.
den 3
ABC üçgeninde kosinüs teoremini uygularsak;
den -bccosA =
ABC üçgeninin alan formülünü uygularsak;
=
dan bcsinA=2 bulunur.
=
+ -b.c.cosA+
bulunur.
b.c.sinA (3) olur.
Bu değerler (3)’te yerine yazılıp formül düzenlenirse
bulunur.Bu eşitlik a,b,c değerlerine göre simetrik olduğundan dolayı aynı işlemleri [FD] ve [ED]
kenarları için yaparsak aynı sonuç elde edilir.Demek ki
dir ve DEF üçgeni
eşkenardır.
YÖNTEM :
Bu proje boyunca doğrudan ispat uygulanmıştır.
ABCD dörtgeninde
olsun. ABCD dörtgeninin kenarlarının
=a,
üzerine üçgenin dışına doğru DCE,DAL,ABF ve BKC eşkenar üçgenleri yerleştirilir ve bu
üçgenlerin ağırlık merkezleri
ve
m(
,
,
ve
dörtgeni eşkenar dörtgendir.
ise
içinde bulundukları üçgenlerin içaçıortay doğruları olduklarından
=
dir. Bundan dolayı m(
)=
dir.
üçgeninde kosinüs teoreminden,
(4)
uzunluğu DAL eşkenar üçgenin ve
bulunur.
uzunluğu DEC eşkenar üçgenin
yüksekliğinin 2/3’ü olduğundan;
=
.
=
ve
.
=
=
tür.
Bu değerleri (4) eşitliğinde yerine yazarsak;

bulunur.
,
üçgenleri
ve
yaptığımızda
=
=
üçgenine eş olduğundan aynı işlemleri
=
buluruz.
üçgeninin iç açılarının toplamını yazarsak ;
m(
)+ m(
)+
(5) eşitliğinde m(
üçgenleri
m(
=
‘dan m(
)+ m(
)=
)=
-x olur.
,
) = x dersek m(
üçgenine eş olduğundan
) = m(
)=m(
m(
) = m(
olduğundan
dörtgenin
açılarının toplamından m(
dörtgeninin
m
=
)=
köşesinin açı ölçüsü
dir. m(
=m(
köşesinin açı ölçüsü
+2x dir.
dir.m(
)=
+2x dir.
=m(
ve
)=m(
)=
- x ve
) = m(
)= x
) = x dir.
üçgeninin iç açılarının toplamından m
A
dir. (5)
=
dir. m(
köşesinin açı ölçüsü
dir. m(
üçgeninin iç açılarının toplamından
-x olduğundan
dörtgenin
üçgeninin iç açılarının toplamından m
-x olduğundan
üçgeninin iç
)= x olduğundan
=m(
- 2x dir.D
)=
- 2x dir. C
dörtgeninin
=
köşesinin açı ölçüsü
SONUÇ:
dörtgeninde ;
=
m( )=m(
m( )=m(
=
)=
)=
=
- 2x
+2x
olduğundan tüm kenar uzunlukları birbirine eşit ,karşılıklı açılar eşit ve birbirine bakan açılar
toplamı
olduğundan
dörtgeni eşkenar dörtgendir.
YÖNTEM :
ABCD dörtgeninde
olsun. ABCD dörtgeninin kenarlarının
=a,
üzerine üçgenin içine doğru DCE,DAL,ABF ve BKC eşkenar üçgenleri yerleştirilir ve bu üçgenlerin
ağırlık merkezleri
,
,
ve
üçgeni dik üçgen olduğundan
=
,
dörtgeni eşkenar dörtgendir.
ise
= ,
=
+
=
,
‘dir. (6)
=
dir.
noktası DAL üçgeninin ağırlık merkezi olduğundan dolayı
.
=
=
bulunur.
=
‘den
-
=
-
bulunur.
noktası FAB üçgeninin ağırlık merkezi olduğundan dolayı
.
=
=
=
,
yüksekliğin 2/3 ü kadardır.
bulunur. Bu değerleri (6) denkleminde yerine koyarsak;
‘den
+(
üçgenleri
,
bulunur.
üçgeni ile eş üçgenler olduğundan
bulunur.Yine bu üçgenlerin eşliğinden dolayı
ölçüleri eşittir,
yüksekliğin 1/3’ü kadardır.
ve
dörtgeninin
ve
köşelerinin açı
köşelerinin açı ölçüleri eşittir.
SONUÇ:
Kenarlarının eşit olması,karşılıklı açıların eşit olması, karşı durumlu açıların toplamının
olması
dörtgeninin eşkenar dörtgen olduğunu gösterir.
Geliştirme: Üçgenler üzerinde sağlanan Napoleon Teoreminin dikdörtgen üzerine uyguladığımızda
eşkenar dörtgen oluştuğunu gösterdik.Projenin geliştirilmesinde, düzgün olan diğer çokgenlerde
uygulanabilirliği araştırılabilir.
Kaynaklar:
1) Mustafa Yağcı , 2004 Yaz Matematik Dünyası Dergisi , Geometri Köşesi, syf 74-75-76-77-78
2) John E. Wetzel,1992,Converses of Napoleon’s Theorem.Amer. Math.Monhtly 89,pp.339-351
3) H. Martini , 1996 , On the Theorem of Napoleon and related topics, Math, Semester Ber,
43 , pp.47-64
4) MEB Komisyon,2012, 10.Sınıf Matematik Kitabı, Sayfa 138-195
5) MEB Komisyon,2012, 10.Sınıf Geometri Kitabı,Sayfa 113-153,195-197, 224-227.