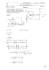π ξ ξ π ξ π ξ ξ ξ π ξ ξ ξ ω π π ξ π ω ω ξω ω ω ξω

π ξ ξ π ξ π ξ ξ ξ π ξ ξ ξ ω π π ξ π ω ω ξω ω ω ξω

ÖRNEK SORU ÇÖZÜMLERİ:
5K
olan negatif birim geribeslemeli bir sistemin birim
s (2Ts + 3)
basamak cevabında 2 s. ’lik bir tepe zamanında %50 ’lik maksimum aşım oluşmaktadır. Buna göre
sistemin sönüm oranını, doğal frekansını, K ve T değerlerini bulunuz.
1-) İleri yol transfer fonksiyonu G ( s ) =
Çözüm: Aşım değeri %50 olarak verilmiş, önce aşım formülünden ξ değeri bulunur:
Mp =e
ξπ
−
(Ln 0.5)
1−ξ 2
2
= 0.50
→
= ξ π + (Ln 0.5) ξ
2
2
ξπ
Ln 0.5 = −
2
2
→
1− ξ 2
ξ=
→
(Ln 0.5)2 (1 − ξ 2 ) = (ξ π )2
(Ln 0.5)2
π 2 + (Ln 0.5)2
= 0.216
Sonra bulunan ξ = 0.216 değeri tepe zamanı formülünde kullanılarak ω n bulunur:
tt =
π
ωn 1 − ξ 2
= 2 s.
→ ωn =
π
tt 1 − ξ 2
=
π
2 1 − (0.216) 2
= 1.61 rad/s.
Hesaplanan ξ ve ω n değerleri karakteristik denklemde kullanılarak K ve T değerleri bulunur:
5K
5K
ω n2
C ( s)
G ( s)
5K
s (2Ts + 3)
2T
=
=
=
=
=
5K
R( s) 1 + G ( s) 1 +
2Ts 2 + 3s + 5K s 2 + 3 s + 5K s 2 + 2ξωn s + ω n2
s (2Ts + 3)
2T
2T
3
= 2ξωn = 2.(0.216)(1.61) = 0.696 → T = 2.155
2T
5K
2.(2.155)(1.61) 2
= ω n2 = (1.61) 2 → K =
= 2.234
2T
5
2-) Şekilde verilen mekanik sisteme giriş olarak f (t ) = 5 N şiddetinde
basamak şeklinde bir kuvvet uygulanmış ve buna karşılık çıkış olarak
kütlenin x(t ) yer değiştirmesi ölçülmüştür. Sistem 2 s. sonra ilk aşıma
ulaşmış olup bu andaki net maksimum aşım miktarı 3.10 −3 m. olarak
ölçülmüştür. Sistemin kalıcı-durum haline ulaştıktan sonraki x(t ) yer
değiştirmesi harekete başlama noktasından itibaren 0.03 m. olarak
ölçülmüştür. Buna göre;
a) Sistemin transfer fonksiyonunu elde ediniz.
b) Sistemin doğal frekansını, sönüm oranını, M , B ve K sabitlerini
bulunuz. Bu sonuçlara göre sistemin ne tür bir dinamik davranış
gösterdiğini yorumlayınız.
c) Sistemin zaman alanı cevabını bulunuz.
f (t )
M
x(t )
K
B
Çözüm:
a) Newton’un hareket denklemine göre, ∑ F = M .a eşitliğini bu sisteme uygularsak:
d 2 x(t )
d x(t )
f (t ) − f B (t ) − f K (t ) = M .a → f (t ) = M
+B
+ K x(t ) ifadesi elde edilir. Bu ifadeye
2
dt
dt
sıfır başlangıç koşulları altında Laplace dönüşümünü uygularsak, transfer fonksiyonu:
X ( s)
1
F ( s ) = M s 2 X ( s ) + B sX ( s ) + K X ( s ) →
=
olarak elde edilir
2
F ( s ) Ms + Bs + K
1
b) Sistem cevabının oturduğu değer: 0.03 m, net aşım miktarı: 0.003 m, maksimum aşıma ulaşma zamanı
tt = 2 s. olarak ölçülmüş. Buna göre,
c(t ) − c(∞) 0.003
=
= 0.1 olarak bulunur. Bu değer aşım formülünde yerine koyulursa:
Mp = t
c (∞ )
0.03
Mp =e
−
ξπ
1−ξ 2
= 0.1
→
ξπ
Ln 0.1 = −
(Ln 0.1)2 = ξ 2π 2 + (Ln 0.1)2 ξ 2
1−ξ
ξ=
→
2
(Ln 0.1)2 (1 − ξ 2 ) = (ξ π )2
→
(Ln 0.1)2
π 2 + (Ln 0.1)2
= 0.6 < 1
Burada ξ < 1 olduğu için sistem %10 aşım yapmıştır ve salınımlı sönümlü bir cevap vermiştir.
Sonra bulunan ξ = 0.6 değeri tepe zamanı formülünde kullanılarak ω n bulunur:
tt =
π
ωn 1 − ξ 2
= 2 s.
→ ωn =
π
tt 1 − ξ 2
=
π
2 1 − (0.6) 2
= 1.96 rad/s.
M , B ve K sabitlerini bulmak için sistemin karakteristik denklemi kullanılarak:
B
K
B
K
= s 2 + 2ξωn s + ω n2 →
= 2ξωn ve
= ω n2 eşitlikleri yazılabilir.
s2 +
s+
M
M
M
M
Bulunun eşitliklerden M , B ve K sabitlerini hesaplayabilmek için ilave olarak Laplace dönüşümünün
son değer teoremi kullanılır. Burada giriş işaretinin Laplace dönüşümü
5
f (t ) = 5 N → F ( s ) =
olup
s
X ( s)
1
5 5
x(∞) = Lim x(t ) = Lim sX ( s ) = Lim s
F ( s) = Lim s/
⋅ = = 0.03 → K = 166.67 N/m
2
t →∞
s →0
s →0
s →0
F ( s)
Ms + Bs + K s/ K
olarak elde edilir. Bulunan K değeri aşağıdaki eşitliklerde yerine koyularak B ve K değerleri hesaplanır
K
K 166.67
= ω n2 → M = 2 =
= 43.38 kg
M
ω n (1.96) 2
B
= 2ξωn
M
→ B = M .2ξωn = (43.38)2(0.6)(1.96) = 102.04 N/(m/s)
c) Sistemin cevap fonksiyonu, sistemin transfer fonksiyonu ile giriş işaretinin Laplace dönüşümünün
1
5
çarpımı olarak X ( s) =
⋅
şeklinde yazılır. Sistemin zaman alanı cevabı, sistemin cevap
2
Ms + Bs + K s
fonksiyonunun ters Laplace dönüşümünden hesaplanır:
1
5⎫
⎧
⋅ ⎬ = ? (kısmi kesirlere ayırma yöntemiyle hesaplanabilir)
x(t ) = L−1 ⎨ 2
⎩ Ms + Bs + K s ⎭
Sistemin cevap fonksiyonunun paydasının 3 adet kökü vardır. Bunlar: s ( Ms 2 + Bs + K ) = 0 → s1 = 0 ve
2
− B m B 2 − 4MK − 102.04 m (102.04) − 4(43.38)(166.67)
=
= −1.18 m 1.57 j olarak hesaplanır.
2M
2(43.38)
Sistemin cevap fonksiyonu kısmi kesirlere ayrılmış şekilde
Kc
Kc
A
X (s) = +
+
s s + 1.18 − 1.57 j s + 1.18 + 1.57 j
biçiminde yazılır. Zaman alanı cevap fonksiyonu, ters Laplace dönüşümü uygulanarak
1
x(t ) = A u (t ) + K (a + bj ) e at sin(bt + α )
b
s2,3 =
2
şeklini alır. Burada bilinmeyen değerler:
⎡
⎤ 5
5
5
A = Lim ⎢ s/
= =
= 0.03
⎥
2
s →0
⎣ s/ ( Ms + Bs + K ) ⎦ K 166.67
⎡
⎤
5
5
⎡5⎤
=
( Ms 2 + Bs + K )
Lim ⎢ ⎥ =
⎢
⎥
2
s → −1.18 +1.57 j
s ( Ms + Bs + K ) ⎦ s → −1.18 +1.57 j ⎣ s ⎦ − 1.18 + 1.57 j
⎣
5
1.57
K (a + bj ) =
= 2.545 , α = arctan
= 2.215 rad , a = −1.18 , b = 1.57
− 1.18
(−1.18) 2 + (1.57) 2
olarak belirlenir ve sistemin zaman cevabı:
1
x(t ) = A u (t ) + K (a + bj ) e at sin(b t + α )
b
1
= 0.03 u (t ) +
2.545 e −1.18 t sin(1.57 t + 2.215)
1.57
x(t ) = 0.03 u (t ) + 1.621e −1.18 t sin(1.57 t + 2.215)
K (a + bj ) =
Lim
şeklinde elde edilir.
0 .6
C ( s)
= G1 ( s ) =
0.45s + 0.75
R( s)
25
C ( s)
= G2 ( s ) = 2
R( s)
s + 4 s + 25
1.2
a
1
0.8
c(t)
3-) Şekilde negatif geribeslemeli iki farklı sistem
için iki adet birim basamak giriş cevabı eğrisi
verilmiştir. Bu eğrilere ait transfer fonksiyonları
aşağıdaki gibi verilmiştir.
Birim Basamak Cevabı
1.4
0.6
b
0.4
0.2
0
0
0.5
1
1.5
2
2.5
3
3.5
zaman (sec)
a) Eğrilerin dinamik davranış özelliklerine göre hangi transfer fonksiyonunun hangi eğriye ait olduğunu
belirtiniz ve her bir sistem için kazanç katsayısı, zaman sabiti, doğal frekans, sönüm oranı gibi dinamik
davranış parametreleri ve varsa kalıcı-durum hatalarını hesaplayınız.
b) Eğriler üzerinden ölçülen değerlerle a) şıkkında istenenleri hesaplayınız ve sonuçları karşılaştırınız.
Çözüm:
a) G1 ( s ) , 1. derece transfer fonksiyonu olduğu için b eğrisine aittir. G2 ( s ) , 2. derece transfer fonksiyonu
olduğu için a eğrisine aittir.
G1 ( s ) ’nin sistem kazancı ve zaman sabiti:
0.6
0.6 / 0.75
0.8
Ks
G1 ( s ) =
=
=
=
→ K s = 0.8 , τ = 0.6 s olarak hesaplanır.
0.45s + 0.75 0.45 / 0.75 s + 1 0.6s + 1 τ s + 1
Şekilden de görüldüğü gibi G1 ( s ) sisteminin birim basamak cevap eğrisinde kalıcı durum hatası vardır.
Bu değer transfer fonksiyonu kullanılarak
⎛ C (s) ⎞
E ( s) R( s) C ( s)
⎟⎟ R( s) olmak üzere
E ( s) = R( s) − C ( s) →
=
−
→ E ( s ) = ⎜⎜1 −
R( s) R( s) R( s)
⎝ R( s) ⎠
⎛ C (s) ⎞
⎟⎟ R( s ) formülünden hesaplandığında
ekd = Lim e(t ) = Lim sE ( s ) = Lim s⎜⎜1 −
t →∞
s→0
s→0
⎝ R( s) ⎠
⎛
Ks ⎞ 1
K
⎟⎟ = 1 − s = 1 − 0.8 = 0.2 olarak bulunur.
ekd = Lim s/ ⎜⎜1 −
s →0
1
⎝ τ s + 1 ⎠ s/
3
25
K s .ωn2
=
transfer fonksiyonundan karakteristik denklem kullanılarak
s 2 + 4 s + 25 s 2 + 2ξωn s + ωn2
G2 ( s ) =
doğal frekans: ωn2 = 25 → ωn = 25 = 5 rad/s
4
4
=
= 0.4 olarak bulunur.
sönüm oranı: 2ξωn = 4 → ξ =
2ωn 10
C ( s)
R( s ) formülüne göre
sistem kazancı: c(∞) = Lim c(t ) = Lim sC ( s ) = Lim s
t →∞
s →0
s →0
R( s)
c(∞) = Lim s/
s→0
K sωn2
s 2 + 2ξωn s + ωn2
⋅
1
=1 →
s/
K s = 1 olarak hesaplanmaktadır.
Şekilden de görüldüğü gibi G2 ( s ) için kalıcı durum hatası ekd = 0 ’dır. Çünkü G2 ( s ) ’nin sistem kazancı
K s = 1 olup sistemin birim basamak cevabı:
C ( s)
c(∞) = Lim c(t ) = Lim sC ( s ) = Lim s
R( s ) formülüne göre
t →∞
s →0
s →0
R( s)
25
1
⋅ = 1 değerine oturmaktadır ve kalıcı durum hatası:
c(∞) = Lim s/ 2
s→0
s + 4 s + 25 s/
⎛ C ( s) ⎞
⎟⎟ R( s) formülünden
ekd = Lim e(t ) = Lim sE ( s) = Lim s⎜⎜1 −
t →∞
s→0
s→0
⎝ R( s) ⎠
25
⎛
⎞ 1
ekd = Lim s/ ⎜1 − 2
⎟ ⋅ = 1 − 1 = 0 olmaktadır.
s →0
⎝ s + 4s + 25 ⎠ s/
b) Eğriler üzerinden ölçülen değerleri kullanarak a) şıkkında istenenler:
1. derece sistem için zaman sabiti, sistem cevabının kalıcı durumdaki değerinin %63.2 ’sine ulaşması için
geçen süre olarak tanımlanır. Şekildeki b eğrisine göre sistem cevabının kalıcı durumdaki değeri 0.8’dir.
Çıkış işaretinin kalıcı durumdaki değerin 0.632 katına ulaşması için geçen süre zaman sabiti olarak
tanımlanır. Çıkış işaretinin (0.632).(0.8) = 0.5 değerine ulaştığı süre, yani zaman sabiti eğriden τ ≅ 0.6 s.
olarak okunur.
Birim basamak giriş işareti için sistem cevabı 0.8 değerine oturmuştur, okunan bu değere göre sistem
kazancı K s = 0.8 ’dir.
Kalıcı-durum hatasının: ekd = Lim e(t ) = Lim[r (t ) − c(t )] = 1 − 0.8 = 0.2 olduğu şekilden de görülmektedir.
t →∞
t →∞
Ks
0.8
=
olarak elde edilir.
τ s + 1 0.6s + 1
Şekildeki a eğrisine göre sistem cevabının kalıcı durumdaki değeri 1’dir. Birim basamak giriş işareti için
sistem cevabı 1 değerine oturmuştur, okunan bu değere göre sistem kazancı K s = 1 ’dir.
Kalıcı-durum hatasının: ekd = Lim e(t ) = Lim[r (t ) − c(t )] = 1 − 1 = 0 olduğu şekilden de görülmektedir.
Grafikten okunan değerlerle sistemin transfer fonksiyonu: G1 ( s ) =
t →∞
t →∞
Şekildeki a eğrisine göre yaklaşık olarak tt = 0.75 s değerinde sistem cevabı c(tt ) = 1.25 değerine
ulaşmaktadır. Eğriden elde edilen bu değerlerden maksimum aşım:
Mp =
c(tt ) − c(∞) 1.25 − 1
=
= 0.25 olarak elde edilir ve sönüm oranı:
c (∞ )
1
Mp = e
−
ξπ
1−ξ 2
= 0.25 →
Ln 0.25 = −
ξπ
1− ξ 2
→
(Ln 0.25)2 (1 − ξ 2 ) = (ξ π )2
4
(Ln 0.25)2 = ξ 2π 2 + (Ln 0.25)2 ξ 2
(Ln 0.25)2
π 2 + (Ln 0.25)2
→ ξ=
= 0.4 olarak bulunur.
Tepe zamanının eğriden okunan tt = 0.75 s değeri ve hesaplanan ξ = 0.4 değeri kullanılarak ω n değeri:
tt =
π
ωn 1 − ξ
2
= 2 s.
→ ωn =
π
tt 1 − ξ
=
2
π
2 1 − (0.216) 2
= 1.61 rad/s. olarak hesaplanır.
Grafikten okunan değerler kullanılarak 2. derece sistemin transfer fonksiyonu:
K s .ωn2
25
olarak elde
G2 ( s ) = 2
= 2
2
s + 2ξωn s + ωn s + 4s + 25
edilir.
Birim Basamak Cevabı
1.2
4-) Şekilde 2. dereceden negatif geribeslemeli bir
sistemin birim basamak giriş cevabı eğrisi verilmiştir.
Bu eğriye göre sistemin kazancını, kalıcı-durum
hatasını, doğal frekansını ve sönüm oranını bulunuz,
sistemin transfer fonksiyonunu yazınız.
1
c(t)
0.8
0.6
0.4
Çözüm:
0.2
2. derece sistemin transfer fonksiyonu:
0
0
1
2
3
4
5
6
C ( s)
K sωn2
= 2
biçimindedir.
zaman (sec)
2
R( s ) s + 2ξωn s + ωn
Birim basamak giriş işareti için sistem cevabı 0.8 değerine oturmuştur, okunan bu değere göre sistem
kazancı K s = 0.8 ’dir. Sistem kazancı birim basamak giriş işareti r (t ) = u (t ) için
C ( s)
c(∞) = Lim c(t ) = Lim sC ( s ) = Lim s
R( s ) formülüne göre
t →∞
s→0
s→0
R( s)
K sωn2
1
⋅ = 0.8 → K s = 0.8 olarak hesaplanır.
2
2
s→0
s + 2ξωn s + ωn s/
Kalıcı-durum hatasının: ekd = Lim e(t ) = Lim[r (t ) − c(t )] = 1 − 0.8 = 0.2 olduğu şekilden de görülmektedir.
c(∞) = Lim s/
t →∞
t →∞
Şekildeki birim basamak cevap eğrisine göre yaklaşık olarak tt = 0.8 s değerinde sistem cevabı
c(tt ) = 1.15 değerine ulaşmaktadır. Eğriden elde edilen bu değerlerden maksimum aşım:
1.15 − 0.8 0.35
Mp =
=
= 0.437 (%43.7) olarak elde edilir ve sönüm oranı:
0.8
0.8
−
Mp =e
ξπ
1− ξ 2
= 0.437 → Ln 0.437 = −
(Ln 0.437 )2 = ξ 2π 2 + (Ln 0.437 )2 ξ 2
ξπ
1−ξ 2
→ ξ=
(Ln 0.437 )2 (1 − ξ 2 ) = (ξ π )2
→
(Ln 0.437 )2
π 2 + (Ln 0.437 )2
= 0.255 olarak bulunur.
Tepe zamanının eğriden okunan tt = 0.8 s değeri ve hesaplanan ξ = 0.255 değeri kullanılarak ω n değeri:
tt =
π
ωn 1 − ξ
2
= 0.8 s.
→ ωn =
π
tt 1 − ξ
2
=
π
0.8 1 − (0.255) 2
= 4.06 rad/s. olarak hesaplanır.
Grafikten okunan değerler kullanılarak 2. derece sistemin transfer fonksiyonu:
K s .ωn2
0.8 (4.06) 2
13.187
G2 ( s ) = 2
=
= 2
2
2
2
s + 2ξωn s + ωn s + 2(0.255)(4.06) s + (4.06)
s + 2.071 s +16.484
olarak elde edilir.
5
5-) Bir elektriksel sisteme ait dinamik denklemler aşağıdaki gibi verilmektedir.
dV (t )
dV (t )
V (t ) − V2 (t )
V (t )
ig (t ) − i1 (t ) = C1 1
, i1 (t ) = 1
, i1 (t ) − i2 (t ) = C2 2
, i2 (t ) = 2
dt
dt
R1
R2
a) Sistemin blok şemasını çiziniz.
b) Blok şemayı indirgeyerek sistemin transfer fonksiyonunu bulunuz ve dinamik davranış parametrelerini
eleman değerleri cinsinden yazınız.
Çözüm:
a) Her bir denklemin Laplace dönüşümünü sıfır başlangıç koşulları altında aşağıdaki gibi yazabiliriz:
dV1 (t )
dt
V (t ) − V2 (t )
i1 (t ) = 1
R1
dV (t )
i1 (t ) − i2 (t ) = C2 2
dt
V (t )
i2 (t ) = 2
R2
ig (t ) − i1 (t ) = C1
→
I g ( s ) − I1 ( s ) = C1 sV1 ( s )
→
I1 ( s ) =
→
I1 ( s ) − I 2 ( s ) = C2 sV2 ( s )
→
I 2 (t ) =
V1 ( s ) − V2 ( s )
R1
V2 ( s )
R2
Elde edilen denklemlere ait blok şemalar aşağıdaki gibi oluşturulabilir:
I g (s )
1
C1s
+
¯
I1 ( s )
I1 ( s )
1
C2 s
+
¯
I 2 (s)
V1 ( s )
V1 ( s )
+
¯
V2 ( s )
V2 ( s )
V2 ( s )
I1 ( s )
1
R1
1
R2
I 2 ( s)
Bu blok şema elemanları sistemin neden sonuç ilişkilerine bağlı olarak birleştirilirse aşağıdaki tüm
sisteme ait blok şema elde edilir.
I g (s )
+
¯
1
C1s
V1 ( s )
+¯
1
R1
I1 ( s )
+
¯
1
C2 s
I 2 ( s)
V2 ( s )
1
R2
1
bloğunun soluna kaydırılarak girişteki fark
C1 s
alıcıyla yer değiştirilmesiyle aşağıdaki blok şema elde edilir:
b) İndirgeme yapabilmek için, ortadaki fark alıcının
6
C1s
I g (s )
1
R1
1
C1s
+¯
+
¯
+
¯
1
C2 s
V2 ( s )
1
R2
İleribesleme yolu üzerindeki 2 iç geribesleme döngüsü indirgendiğinde aşağıdaki blok şema elde edilir:
I g (s )
1
R1C1s + 1
+
¯
V2 ( s )
R2
R2C2+s + 1
¯
C1s
En dıştaki geribesleme döngüsü de indirgendiğinde giriş-çıkış arasındaki ilişki aşağıdaki gibi elde edilir:
I g (s )
R2
2
R1C1 R2C2 s + ( R1C1 + R2C2 + R2C1 ) s + 1
V2 ( s )
Bu sonuca göre sistemin transfer fonksiyonu aşağıdaki gibi yazılabilir:
V2 ( s )
R2
=
2
I g ( s ) R1C1 R2 C 2 s + ( R1C1 + R2 C 2 + R2 C1 ) s + 1
Sistemin dinamik davranış parametrelerini bulmak için transfer fonksiyonu aşağıdaki gibi düzenlenebilir:
1
K s ω n2
V2 ( s )
R1C1 R2 C 2
=
= 2
R C + R2 C 2 + R2 C1
1
I g ( s)
s + 2ξω n s + ω n2
s2 + 1 1
s+
R1C1 R2 C 2
R1C1 R2 C 2
R2 ⋅
Sistemin dinamik davranış parametreleri ξ ve ω n eleman değerleri cinsinden aşağıdaki gibi yazılabilir:
1
R1C1 R2 C 2
doğal frekans:
ω n2 =
sönüm oranı:
2ξω n =
→ ωn =
R1C1 + R2 C 2 + R2 C1
R1C1 R2 C 2
1
R1C1 R2 C 2
→ ξ=
R1C1 + R2 C 2 + R2 C1
2 R1C1 R2 C 2
Burada K s = R2 sistemin kazancıdır.
7
6-) Aşağıda blok şeması verilen sistemde
a) Gd ( s ) = K p + K d s için sistemin transfer fonksiyonlarını ve cevap fonksiyonunu bulunuz.
b) Gd ( s ) = K p + K d s ve ξωn = 2 olması halinde birim rampa başvuru girişinden doğan kalıcı-durum
hatasının 0.05 olması için K p ve K d ne olmalıdır?
c) Bulunan K p ve K d değerlerine göre sistemin doğal frekans ve sönüm oranını bulunuz ve sistemin
dinamik davranışı hakkında bilgi veriniz.
K
d) Gd ( s ) = K p + K d s + i olması halinde birim rampa bozucu girişten doğan kalıcı-durum hatasının 0.05
s
’ten küçük olması için K i ne olmalıdır?
D(s)
+
R(s )
+
¯
Gd (s )
G (s )
1
s ( s + 1)
+
C (s )
Çözüm:
a) Başvuru girişinden çıkışa kadar olan transfer fonksiyonu: R ( s ) ≠ 0 , D( s ) = 0 için
1
( K p + K d s)
K p + Kd s
CR ( s )
Gd ( s )G ( s )
s ( s + 1)
=
=
= 2
R( s) 1 + Gd ( s )G ( s ) 1 + ( K + K s ) 1
s + (1 + K d ) s + K p
p
d
s ( s + 1)
Bozucu girişten çıkışa kadar olan transfer fonksiyonu: R( s ) = 0 , D( s ) ≠ 0 için
1
CD ( s )
G ( s)
1
s ( s + 1)
=
=
= 2
D( s ) 1 + Gd ( s )G ( s ) 1 + ( K + K s) 1
s + (1 + K d ) s + K p
p
d
s ( s + 1)
Sistemin cevap fonksiyonu:
K p + Kd s
1
C ( s ) = CR ( s ) + CD ( s ) = 2
R( s) + 2
D( s) olarak veya
s + (1 + K d ) s + K p
s + (1 + K d ) s + K p
C ( s) =
[
1
( K p + K d s) R( s) + D( s)
s + (1 + K d ) s + K p
2
]
olarak yazılabilir.
b) ξωn = 2 ve Gd ( s ) = K p + K d s olması halinde sistemin transfer fonksiyonu:
K p + Kd s
K + Kd s
C ( s)
= 2
= 2 p
olur, buradan
R( s ) s + (1 + K d ) s + K p s + 2ξωn s + ωn2
1 + K d = 2ξωn = 2(2) = 4 → K d = 3 olmalıdır.
Birim rampa başvuru girişi için kalıcı-durum hatasını hız hata katsayısını kullanarak hesaplarsak:
K
1
.1 = p = K p
K v = Lim sGd ( s )G ( s ) H ( s ) = Lim s/ (K p + K d s )
1
s/ ( s + 1)
s→0
s →0
1
1
1
= 20 olmalıdır.
=
= 0.05 olması için K p =
ekd =
0.05
Kv K p
8
veya kalıcı-durum hatasını hesaplamanın bir yolu da Laplace dönüşümünün son değer teoremidir:
⎛ C ( s) ⎞
E ( s) R( s) C ( s)
⎟⎟ R( s ) olmak üzere
E ( s) = R( s) − C ( s) →
=
−
→ E ( s ) = ⎜⎜1 −
R( s) R( s) R( s)
⎝ R( s) ⎠
⎛ C (s) ⎞
⎟⎟ R( s ) formülünden hesaplandığında
ekd = Lim e(t ) = Lim sE ( s ) = Lim s⎜⎜1 −
t →∞
s →0
s →0
⎝ R( s ) ⎠
⎛
⎞1
⎛
⎞1
K p + Kd s
s/ ( s + 1)
⎟ 2 = Lim s/ ⎜ 2
⎟ 2 = 1 = 0.05 olması için
ekd = Lim s⎜1 − 2
⎟
s →0 ⎜
s → 0 ⎜ s + (1 + K ) s + K ⎟ s
Kp
d
p ⎠ /
⎝ s + (1 + K d ) s + K p ⎠ s
⎝
1
Kp =
= 20 olmalıdır.
0.05
c) Bulunan K p = 20 ve K d = 3 değerleri için sistemin transfer fonksiyonu yazılarak:
K p + Kd s
K + Kd s
CR ( s )
= 2
= 2 p
eşitliğinden sistemin dinamik davranış parametreleri:
R( s ) s + (1 + K d ) s + K p s + 2ξωn s + ωn2
ωn2 = K p = 20 → ωn = 20 = 4.472 rad/s ve
2ξωn = 1 + K d = 4 → 2ξ (4.472) = 4 → ξ = 0.447 olarak bulunur.
Denetleyicide K p = 20 ve K d = 3 değerlerinin kullanılması durumunda ξ = 0.447 < 1 olur ve basamak
giriş işareti uygulanması durumunda kapalı-çevrim sistem salınımlı sönümlü bir davranış gösterir.
d) Gd ( s ) = K p + K d s +
D( s ) ≠ 0 için
C (s)
D( s )
C (s)
D( s)
Ki
olması halinde bozucu girişten çıkışa kadar olan transfer fonksiyonu R( s ) = 0 ,
s
1
1
G(s)
s ( s + 1)
s ( s + 1)
=
=
=
K
K ⎞ 1
1 + Gd ( s )G ( s )
⎛
s ( s + 1) + K p + K d s + i
1 + ⎜ K p + Kd s + i ⎟
s
s ⎠ s ( s + 1)
⎝
s ( s + 1)
s
olarak hesaplanır.
= 3
s + (1 + K d ) s 2 + K p s + K i
Kalıcı-durum hatasını hesaplamak için Laplace dönüşümünün son değer teoremini kullandığımızda
⎛ C (s) ⎞
⎜⎜ −
⎟ D( s ) olmak üzere
E ( s) = R
(
s
)
−
C
(
s
)
→
E
(
s
)
=
−
C
(
s
)
→
E
(
s
)
=
{
D( s ) ⎟⎠
⎝
0
⎛ C (s) ⎞
⎟⎟ D( s ) formülünden hesaplandığında kalıcı-durum hatası
ekd = Lim e(t ) = Lim sE ( s ) = Lim s⎜⎜ −
t →∞
s→0
s→0
⎝ D( s) ⎠
⎛
⎞1
s/
⎟ 2 = − 1 olarak bulunur.
ekd = Lim s/ ⎜ − 3
2
⎜
⎟
s →0
Ki
⎝ s + (1 + K d ) s + K p s + K i ⎠ s/
Burada kalıcı-durum hatasının negatif çıkmasının sebebi, bozucu girişin + yönünde uygulanmasıdır.
Kalıcı-durum hatasının büyüklük olarak 0.05 değerinden küçük olması için:
1
ekd =
< 0.05 → K i > 20 olması gerekir.
Ki
Not: R( s ) = 0 için bozucu giriş pozitif yönde uygulandığında, bozucu girişten doğan kalıcı-durum hatası
negatif çıkar, negatif yönde uygulandığında ise bozucu girişten doğan kalıcı-durum hatası pozitif çıkar.
9
Belirli bir başvuru girişi için bozucu giriş + yönünde uygulandığında, bozucu giriş sistem cevabını
başvuru girişiyle aynı yönde değiştirir ve sistem cevabının başvuru girişinden büyük olması durumunda
toplam kalıcı-durum hatası ekd = Lim e(t ) = Lim[r (t ) − c(t )] denklemine göre negatif çıkar.
t →∞
t →∞
Belirli bir başvuru girişi için bozucu giriş − yönünde uygulandığında, bozucu giriş sistem cevabını
başvuru girişine göre ters yönde değiştirir ve sistem cevabının başvuru girişinden küçük olması
durumunda toplam kalıcı-durum hatası ekd = Lim e(t ) = Lim[r (t ) − c(t )] denklemine göre pozitif çıkar.
t →∞
t →∞
7-) Karakteristik denklemi s + Ks + 2 s + ( K + 1) s + 10 = 0 olarak verilen sistemi kararlı yapan K
kazanç aralığını bulunuz.
4
3
2
Çözüm: s 4 + Ks 3 + 2 s 2 + ( K + 1) s + 10 = 0 → Gerek şarta göre: K > 0 ve K > −1 olmalı
10
Yeter şarta göre:
1
2
→ K >0
K
K +1
K −1
2 K − ( K + 1) K − 1
=
→
> 0 → K >1
10
s2
K
K
K
K −1
K −1
( K + 1) − 10 K
→
( K + 1) − 10 K > 0
K
1
K
s
K −1
− 9 K 2 − 1 > 0 → K 2 > 0 olduğu için
K
bu şartı sağlayan K değeri yoktur.
10
s0
− 9 K 2 − 1 katsayısı bütün K değerleri için negatiftir ve sistem bütün K değerleri için kararsızdır.
− 9 K 2 − 1 > 0 şartını sağlayan bir K değeri olmadığı için sistem K ile kararlı hale getirilemez.
s4
s3
8-) Blok şeması aşağıda verilen kapalı-çevrim sistemi kararlı yapan K kazanç aralığını bulunuz.
R(s)
+
¯
C ( s)
1
K
s
s 3 + 3s 2 + s + 5
s +1
Çözüm:
Sistemin karakteristik denklemi:
1 + G ( s) H ( s) = 1 +
K
s +1
⋅ 3
=0
s s + 3s 2 + s + 5
olup gerekli
s ( s 3 + 3s 2 + s + 5) + K ( s + 1)
= 0 → s 4 + 3s 3 + s 2 + ( K + 5) s + K = 0
3
2
s( s + 3s + s + 5)
4
3
2
olarak yazılabilir. s + 3s + s + ( K + 5) s + K = 0 → Gerek şarta göre: K > 0 ve K > −5 olmalı
düzenleme yapıldığında:
s4
s3
1
3
1
K +5
K
0
Yeter şarta göre: 1. sütundaki elemanların
pozitif olma koşulları aşağıdaki gibi bulunur:
K +2
−
> 0 → K < −2
3
3− K −5
K +2
=−
→
K
3
3
K +2
K +2
−
( K + 5) − 3K
−
( K + 5) − 3K > 0
3
1
3
→
s
K +2
−
K 2 + 16 K + 10 < 0 → − 15.35 < K < −0.65
3
→ K >0
K
s0
Birinci sütundaki elemanların hepsini birden pozitif yapan ortak bir K aralığı olmadığı için kapalı-çevrim
sistem K ile kararlı hale getirilemez. Şekildeki kapalı-çevrim sistem bütün K değerleri için kararsızdır.
s2
10